how to draw the number 4 in 3d
I am an online writer who enjoys writing about mathematics and science.

Canva
In this article nosotros will come across how to depict a 2-dimensional representation of a four-dimensional object.
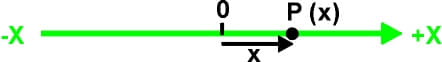
Fig. 1. The number line showing 1D space
Fig. one shows the x-centrality or number line. This is a unmarried dimension. Whatsoever point on the line is represented by a single number (+ten or -x) that indicates its altitude from the origin (0).
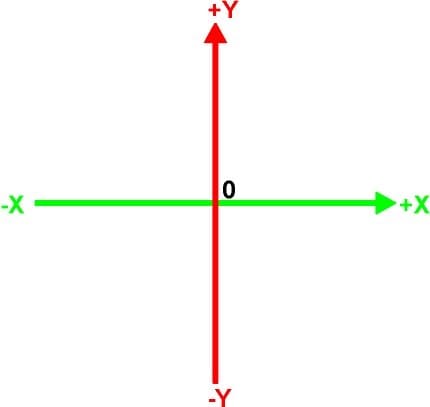
Fig. 2. X and Y axes of 2D infinite
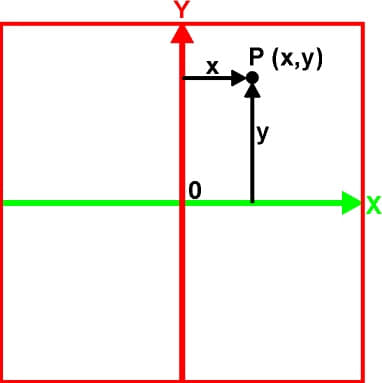
Fig. 3. One plane of 2D space
Fig. iii shows the x,y aeroplane, indicted by a square that contains the x,y axes of second infinite. These axes are xc degrees to each other. Whatsoever point on the plane is located by two numbers (ten,y). X is the distance from the y-axis to the betoken. Y is the distance from the x-centrality to the point. The second coordinate organization is a single airplane.
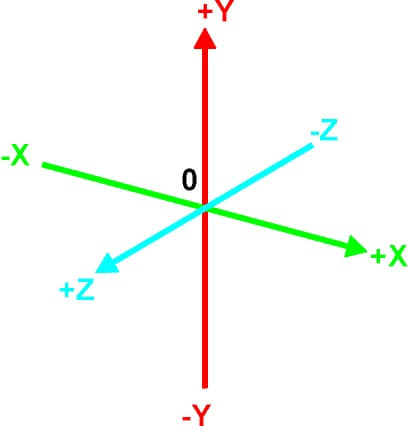
Fig. iv. The 10, Y, and Z axes of 3D space
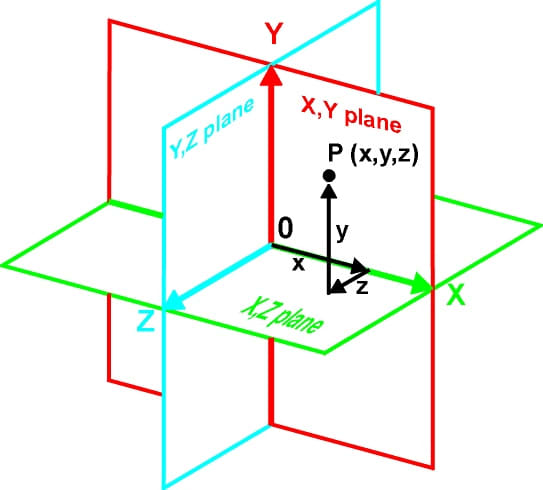
Fig. five. The three planes of 3D infinite.
Whatever point in 3D space is located past three numbers (10,y,z). The 3D coordinate system consists of three planes. Hither these planes are indicated by squares and they are each xc degrees to each other. Because we are viewing the planes at an bending and their image is flattened to the 2nd surface of the page, the squares practice not look like squares and the angles exercise not appear to be xc degrees. However, we are used to seeing squares at an angle and can have the drawing as representing three perpendicular squares.
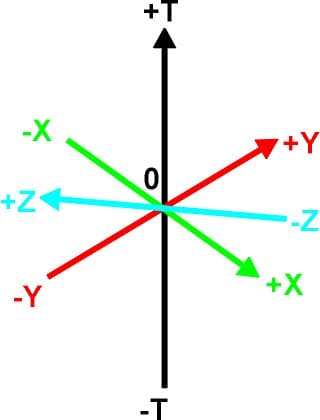
Fig. vi. The four mutually perpendicular axes of 4D space. These can represent three spatial axes and one time centrality or iv spatial axes ten,y,z,westward
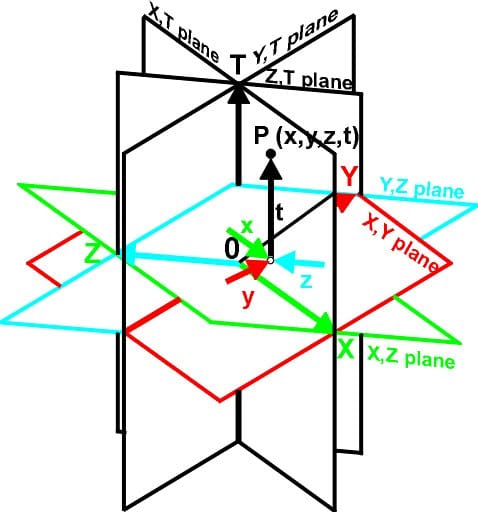
Fig. vii. The three 3D planes on their 4D axes.
The 4D coordinate arrangement consists of half dozen planes. This equals all the paired combinations of the axes, xy, xz, xw, yw, zw and yz. That is the number of combinations of due north objects taken r at a time = n!/r!(n-r)! = 4!/2!(4-2)! = 24/4 = 6.
Just every bit the 3D planes appear distorted when projected on a 2nd surface, these planes in four dimensions are fifty-fifty more distorted when projected on a 2D surface. Fig. 7 shows the second projection of the six planes that described 4D space. Whatever point in 4D infinite is located past four numbers (x,y,z,t). A representation of 4D infinite is similar a time-exposed photo since each 3D section occurs at a dissimilar instant in time. This -D infinite is the Minkowski space when the Lorentz transformations are used with this coordinate system.
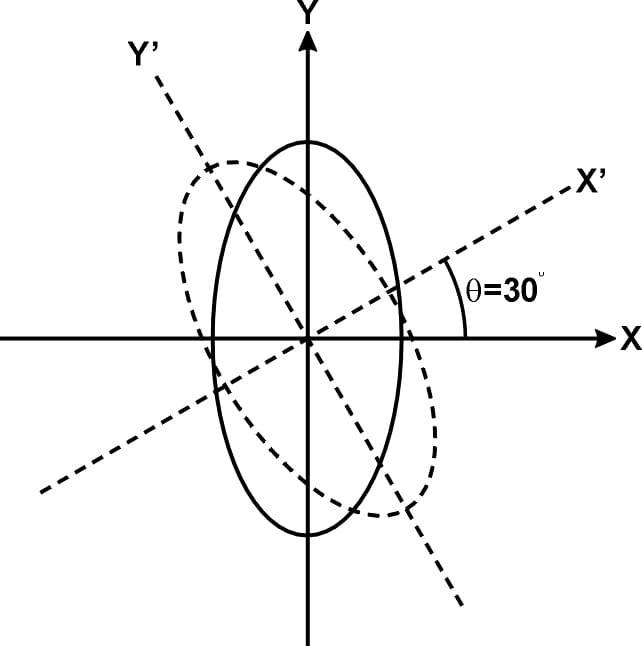
Fig 8. The rotation of a 2d effigy on a unmarried plane.
Read More than From Feltmagnet
In analectic geometry there are 2 combined equations used for rotating all the 2D points in an object by the angle q, on the x,y airplane. These equations are
x' = x*cos q – y*sin q
and
y' = x*sin q +y*cos q
Using the Equations for the 3D Figure
By expanding these two equations into half-dozen equations and using points indicated by three numbers, we produce a 2D representation of a 3D object. When one plane is rotated the whole figure is rotated by the same amount. By using three dissimilar angles of rotation this representation of a three-dimensional object can be viewed from any angle.
Algorithm that produces the 3D effect:
XA=10*COS(A1)-Y*SIN(A1):
YA=X*SIN(A1)+Y*COS(A1)
XB=XA*COS(A2)-Z1*SIN(A2)
ZA=XA*SIN(A2)+Z1*COS(A2)
ZB=ZA*COS(A3)-YA*SIN(A3)
YB=ZA*SIN(A3)+YA*COS(A3)
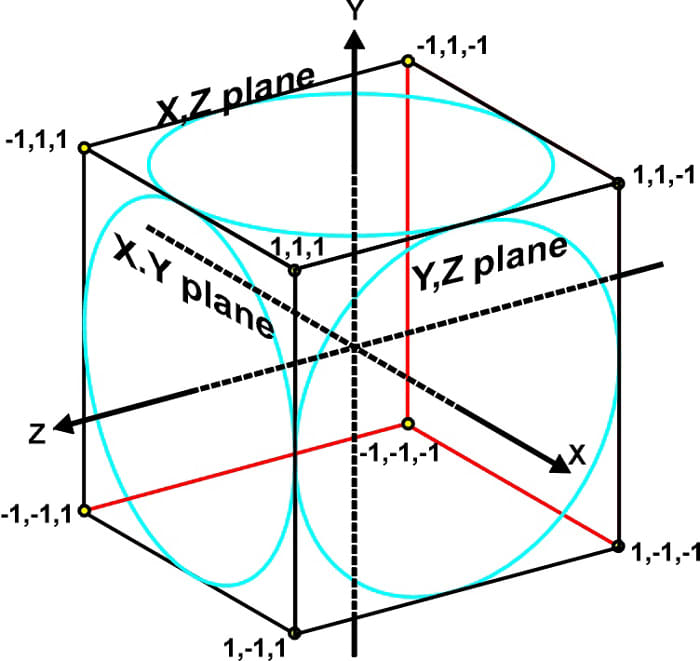
Fig. 9. A cube is a 3D object.
Using the Equations for the 4D Figure
By expanding these two equations into 12 equations and using points indicated past four numbers, we produce a 2nd representation of a 4D object. By rotating any or all of the six planes of the 4D object, the representation of a four-dimensional object can be viewed from whatsoever angle.
Algorithm that produces 4D image:
ZA=Z*CQS(A1)-West*SIN(A1)
WA=Z*SIN(A1)+West*COS(A1)
YA=Y*COS(A2)-WA*SIN(A2)
WB=Y*SIN(A2)+WA*COS(A2)
XA=Ten*COS(A3)-ZA*SIN(A3)
ZB=X*SIN(A3)+ZA*COS(A3)
XB=XA*COS(A4)-WB*SIN(A4)
WC==XA*SIN(A4)+WB*COS(A4)
YB=YA*COS(A5)-ZB*SIN(A5)
ZC=YA*SIN(A5)+ZB*COS(A5) :
XC=XB*COS(A6)-YB*SIN(A6)
YC=XB*SIN(A6)+YB*COS(A6)
X2=Chiliad*(Xc+Ninety*ZC/800+Xc*WC/800)+158:REM adds perspective to ten(thousand=calibration)
Y2=0.8*K* (YC+YC*ZC/800+YC*WC/800)+100:REM adds perspective to y(k=scale)
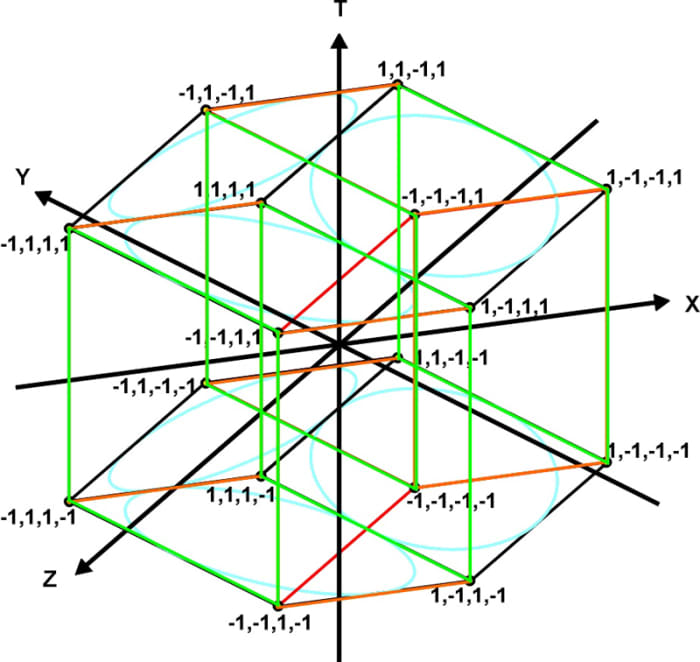
Fig. 10. Tesseract or four dimensional hypercube
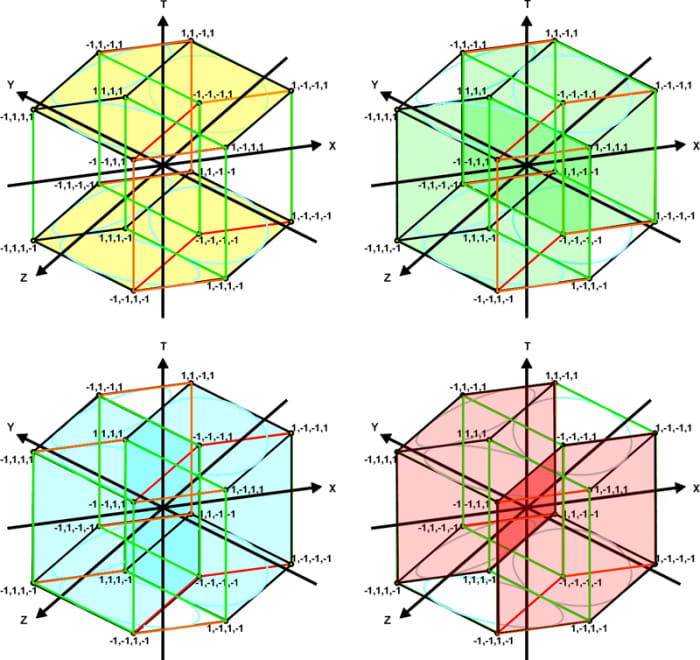
Fig. 11. The hypercube is composed eight interlaced 3D cubes
The Estimator Program 4D-CUBE Draws the Tesseract
This program draws a two-dimensional representation of a four-dimensional hypercube. Each of the 16 points or vertices are indicated past iv numbers. One number for the x-axis, the y-centrality, the z-centrality and the w-axis. The 32 edges are indicated by drawing a line between two vertices.
Figs. 12 and 13 testify the hypercube at different degrees of rotation. Fig. xiv shows the hypercube with no rotation effectually any axis. Because the plan has a perspective factor in information technology fig. xiv appears equally three connected squares. Without perspective fig. 14 would appear as a single square but as a 3D cube does. In GW Basic the elevation of the pixels is greater than the width. When figures are viewed on the screen they are taller than they should exist. Past multiplying the final y by 0.8, these drawings have been adjusted then that the superlative and the width are proportionally corrected.
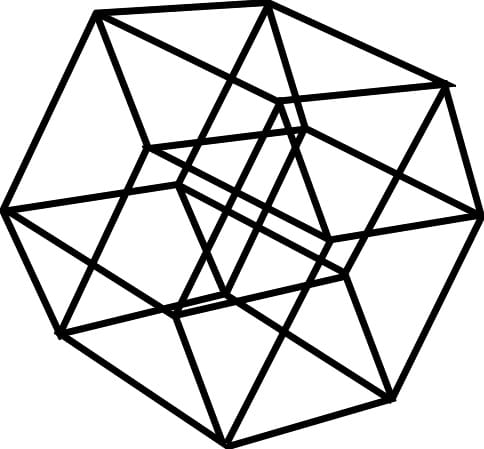
Fig. 12
4D hypercube and the rotation of each aeroplane
ROTATION OF ZW Airplane 10°
ROTATION OF YW Airplane 20°
ROTATION OF XZ Aeroplane 30°
ROTATION OF XW PLANE 40°
ROTATION OF YZ PLANE 50°
ROTATION OF XY PLANE 60°
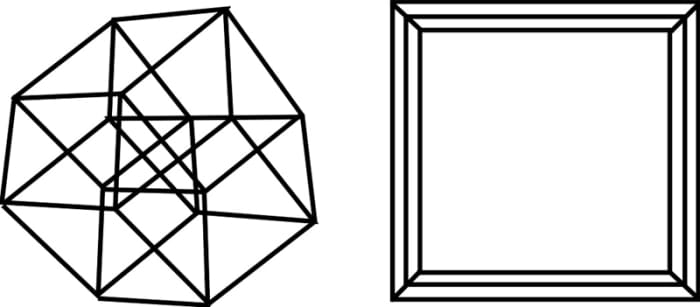
Fig. 13 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Fig 14
4D hypercube and rotation of planes . . . 4D hypercube and rotation of planes
ROTATION OF ZW Airplane l° . . . . . . . . ROTATION OF ZW Airplane 0°
ROTATION OF YW Plane 50° . . . . . . . ROTATION OF YW PLANE 0°
ROTATION OF XZ Plane l° . . . . . . . . ROTATION OF XZ Aeroplane 0°
ROTATION OF XW PLANE 0° . . . . . . . . ROTATION OF XW Plane 0°
ROTATION OF YZ Airplane 0° . . . . . . . . ROTATION OF YZ Plane 0°
ROTATION OF XY PLANE 0° . . . . . . . . ROTATION OF XY PLANE 0°
The Reckoner Program 4D-CUBE in GW Basic
100 CLS:REM 4D-CUBE 110 DIM X(300)
120 DIM Y(300)
130 DIM Z(300)
140 DIM W(300)
150 INPUT "Calibration (advise 1)";K
160 INPUT "ROTATION OF ZW Plane IN DEGREES";Al
170 INPUT"ROTATION OF YW Airplane IN DEGREES";A2
180 INPUT "ROTATION OF XZ PLANE INDEGREES";A3
190 INPUT "ROTATION OF XW PLANE IN DEGREES";A4
200 INPUT "ROTATION OF YX Aeroplane IN DEGREES";A5
210 INPUT "ROTATION OF XY Airplane IN DEGREES";A6
230 A1=A1/57.29577951 converts degrees to radians
240 A2=A2/57.29577951
250 A3=A3/57.29577951
260 A4=A4/ 57,29577951
270 A5=A5/57.29577951
280 A6=A6/57.29577951
290 SCREEN 1,0: CLS:KEY OFF:Color 0,i 320 FOR North=I TO 2
330 READ X,Y,Z,Due west:REM reads information
340 IF 10=1.000 THEN 530
350 ZA=Z*CQS(A1)-Westward*SIN(A1) :REM Algorithm that produces 4D image
360 WA=Z*SIN(A1)+West*COS(A1)
370 YA=Y*COS(A2)-WA*SIN(A2)
380 WB=Y*SIN(A2)+WA*COS(A2)
390 XA=10*COS(A3)-ZA*SIN(A3)
400 ZB=X*SIN(A3)+ZA*COS(A3)
410 XB=XA*COS(A4)-WB*SIN(A4)
420 WC==XA*SIN(A4)+WB*COS(A4)
430 YB=YA*COS(A5)-ZB*SIN(A5)
440 ZC=YA*SIN(A5)+ZB*COS(A5) :
450 XC=XB*COS(A6)-YB*SIN(A6)
460 YC=XB*SIN(A6)+YB*COS(A6)
470 if n=ane and then 540
480 X2=K*(90+XC*ZC/800+XC*WC/800)+158:REM adds perspective to 10(k=scale)
490 Y2=0.8*Thousand* (YC+YC*ZC/800+YC*WC/800)+100:REM adds perspective to y(k=scale)
500 Side by side Northward
505 IF W=twoscore Then 1000: REM highlights 1 3D cube
510 LINE (X1, Y1)-(X2,Y2),3:REM draws figure
520 GOTO 320
530 END
540 X1=K* (Xc+Xc*ZC/800+XC*WC/800)+158:REM adds perspective to x(k=scale)
550 Y1=0.8*K*(YC+YC*ZC/800+YC*WC/800)+100:REM adds perspective to y(k=scale)
560 GOTO 500
600 DATA -twoscore,-twoscore,40,-40,twoscore,-xl,40,-40
610 Information -40, -40, 40, 40, xl, -40, xl, 40
620 Data 40,-xl,40,-40,40,forty,40,-40
630 DATA 40,-xl/40,40,xl,40,40,40
640 Data 40,xl,40,-xl,-xl„xl,xl,-40
650 DATA twoscore,40,40,xl,-xl,xl,twoscore,40
660 Data -40,40,40,-forty,-40,-40,twoscore,-40
670 Data -40 ,40. 40, 40, -xl, -40, xl, 40
680 DATA -40,-xl,-40,-40,40,-40,-xl,-40
690 DATA -40, -40, -40, 40, forty, -40, -40, 40
700 DATA 40,-forty,-forty,-xl,40,40,-twoscore,-forty
710 DATA 40,-40,-40, twoscore, 40, 40,-40, xl
720 Data 40, 40, -40, -twoscore, -40, forty, -40, -forty
730 Data twoscore,40,-forty,xl,-40,xl,-twoscore,xl
740 Data -40,40,-40,-40,-40,-forty,-twoscore,-forty
750 Information -twoscore,40,-40,forty,-40,-40,-40,40
760 Information -40, -xl, xl, -40, -twoscore,-xl,-40,-twoscore
770 Data -40,-xl,40,forty,-xl,-forty,-xl,forty
780 DATA 40, -40, 40, -twoscore, twoscore, -xl, -40, -40
790 Data forty, -xl, 40, xl, forty, -40, -twoscore, forty
800 Data twoscore, 40,twoscore,-forty,40,xl,-twoscore,-40
810 DATA forty,40,twoscore,40,40,twoscore,-40,40
820 Information -forty,forty,40,-40,-40,40,-xl,-40
830 DATA -40, 40, 40,xl, xl , 40, -twoscore, 40
840 DATA -xl,-forty,40,-40,-twoscore,-40,twoscore,40
850 Data xl,-40,40,-40,40,-40, forty,40
860 Data 40,twoscore,40,-40,40,40,40,forty
870 DATA -twoscore,twoscore,40,-40,-40,40,xl,40
880 DATA -forty,-40,-40,-xl,-40,-40,-40,forty
890 Data 40,-40, -40, -forty, 40, -40, -40, xl
900 Information 40,40,-40,-xl,40,40,-40,40
910 Information -xl,40,-twoscore,-40,-forty, twoscore,-forty, 40
920 DATA 1000,1000,thousand,k
thou LINE(X1,Y1)-(X2,Y2),2
1010 GOTO 320
The Reckoner Program 4D-Plane
This program draws a ii-dimentional representation of the half-dozen planes of the iv axes. Fig. 15 shows the six planes and the coordinates in 4D space. A layout like this is helpful before cartoon any 4D figure. By using vi dissimilar angles of rotation this representation of four-dimensional planes can be viewed from any angle. When all the angles are at null nosotros see the x.y plane equally a square. All the other planes are edge-on.
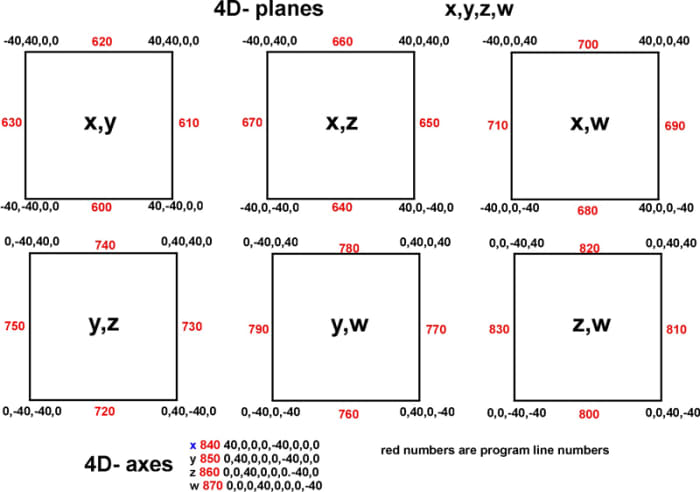
Fig 15. The six planes of 4D infinite
Fig. 15 lays out all the points in the 4D coordinate organization. These are used in the computer program 4D-PLANE
In figs. 16 to 18 nosotros meet 3D planes are drawn with blue lines, while all the planes containing the w-axis are fatigued in red. When nosotros run the computer program the 3D planes are drawn with white lines while all the planes containing the w-axis are drawn in purple. In GW Basic the height of the pixels is greater than the width. When figures are viewed on the screen they are taller than they should be. By multiplying the final y by 0.eight, these drawings have been adjusted so that the height and the width are proportionally corrected.
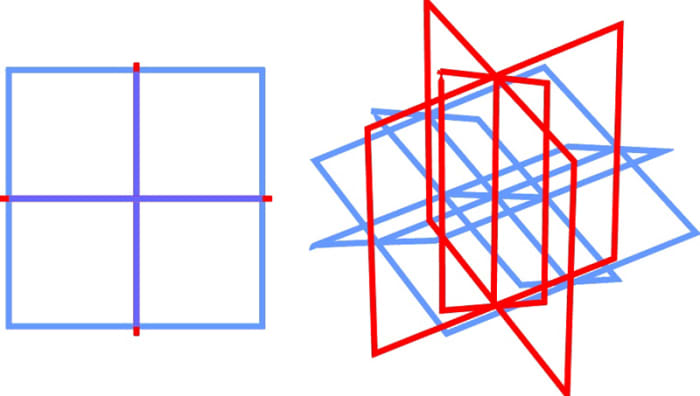
Fig.16. . . . . . . . . . . . . . . . . . . . . . . . . . . . . Fig. 17
4D planes and the rotation of planes 4D planes and the rotation of planes
ROTATION OF ZW PLANE 0° . . . . . . . . ROTATION OF ZW Aeroplane 0°
ROTATION OF YW Plane 0°. . . . . . . . ROTATION OF YW Plane 0°
ROTATION OF XZ Airplane 0° . . . . . . . . ROTATION OF XZ PLANE 30°
ROTATION OF XW Aeroplane 0° . . . . . . . ROTATION OF XW Airplane 50°
ROTATION OF YZ PLANE 0° . . . . . . . .ROTATION OF YZ Plane 70°
ROTATION OF XY PLANE 0° . . . . . . . . ROTATION OF XY Aeroplane 90°
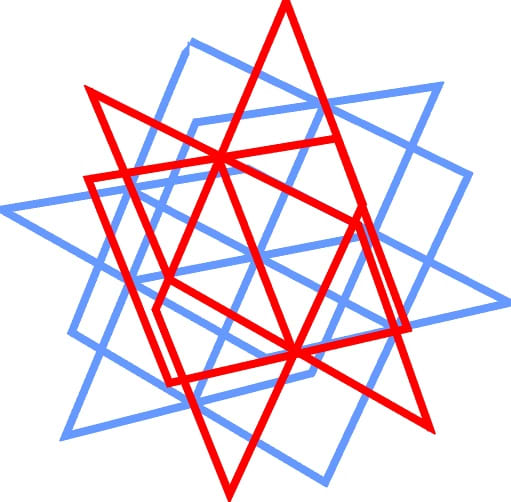
Fig. 18
4D coordinate planes and the rotation of each plane
ROTATION OF ZW Aeroplane 10°
ROTATION OF YW Plane twenty°
ROTATION OF XZ Aeroplane thirty°
ROTATION OF XW PLANE twoscore°
ROTATION OF YZ PLANE 50°
ROTATION OF XY PLANE 60°
This figure is complex and difficult to visualize. To assist in the visualization of this effigy, fig. nineteen is separated into two parts. Commencement are the 3D planes with the ten,y,z centrality. Second are the planes containing the w axis.
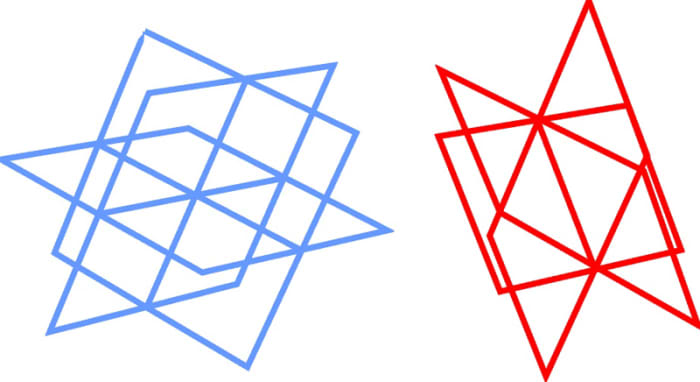
Fig. 19. Two parts of a 4D coordinate system.
Computer Program 4D-PLANE
100 CLS:REM 4D-PLANE
110 DIM XC300) . 120 DIM Y(300) 130 DIM Z(300) 140 DIM W(300) 150 INPUT "SCALE";K
160 INPUT "ROTATION OF ZW Plane IN DEGREES";Al
170 INPUT "ROTATION OF WY Aeroplane IN DEGREES";A2
180 INPUT "ROTATION OF XZ PLANE IN DEGREES"; A3
190 INPUT "ROTATION OF XW Plane IN DEGREES";A4
200 INPUT "ROTATION OF YZ Plane IN DEGREES";A5
210 INPUT "ROTATION OF XY PLANE IN DEGREES";A6
230 A1=A1/57. 2957795* :REM converts degrees to radians
240 A2=A2/57.29577951*
250 A3 =A3/57. 29577951*
260 A4=A4/57.29577951*
270 A5=A5/57,29577951*
280 A6=A6/57.29577951*
290 SCREEN 1,0:CLS:Key OFF:Colour 0,1
320 FOR.N=i TO 2
330 READ X,Y,Z,W
340 IF 10=1000 THEN 530
350 ZA=Z*COS(A1)-W#SIN(A1):REM algorithms to produce 2D representation of 4D object
360 WA=Z*SIN(A1)+Westward*COS(A1)
370 YA=Y*COS(A2)-WA*SIN(A2)
380 WB=Y*SIN(A2)+WA*COS(A2)
390 XA=Ten*COS(A3)-ZA*SIN(A3)
400 ZB=X*SIN(A3)+ZA*COS(A3)
410 XB=XA*COS(A4)-WB*SIN(A4)
420 WC=XA*SIN(A4)+WB*COS(A4)
430 YB=YA*COS(A5)-ZB*SIN(A5)
440 ZC=YA*SIN(A5)+ZB*COS<A5)
450 Ninety=XB*COS(A6)-YB*SIN(A6)
460 YC=XB*SIN(A6)+YB*COS(A6)
470 IF N=l THEN 540
480 X2=K*(90+XC*ZC/800+XC*WC/800)+158
490 Y2=0.8*M*(YC+YC*ZC/800+YC*WC/800)+100
500 NEXT N
505 IF Due west= 40 OR West= -40 And then 1000
510 LINE (X1,Y1)-(X2,Y2),3
520 GOTO 320
530 END
540 X1=K*(XC+XC*ZC/800+90*WC/800)+158
550 Y1=0.viii*Grand*(YC+YC*ZC/8OO+YC*WC/800)+100
560 GOTO 500
600 DATA - forty,- 40„0,0 , 40,- 40,0,0
610 DATA 40,- forty,0,0,40,xl,0,0
620 Information 40,40,0,0,-40,40,0,0
630 DATA - 40,40,0,0,- 40,- forty,0,0
640 Data - 40 ,0,xl, 0, 40, 0., - 40, 0
650 Data 40, 0,- 40,0,xl,0, 40,0
660 Information - 40,0,twoscore,0 , 40,0,40, 0
670 Information - forty, 0, 40, 0, - xl, 0, - 40, 0
680 Information 0, - 40, - 40, 0, 0, xl, - 40, 0
690 DATA 0,40,- 40,0,0,xl,40,0
700 DATA 0,40,40,0,0, - 40, 40, 0
710 DATA 0,- twoscore, xl, 0,0,- 40,,- 40,0
720 Information - forty,0,0,- 40,40,0,0,-xl
730 DATA 40,0,0,- 40,40,0,0,40
740 Data 40,0,0,40,- 40,0,0,40
750 Information - xl,0.0,twoscore,- twoscore,0,0,- 40
760 DATA 0,- xl,0,- forty,0,40,0,- 40
770 Information 0,0, 0, - 40 , 0, 40, 0, 40
780 DATA 0,xl.0, forty,.0,xl,0,40
790 Data 0, -40, 0, 40, 0, -40,, 6, - forty
800 Data 0,0, 40, - 40, 0, 0, - forty, - twoscore
810 DATA 0,0,40, 40, 0., 0, 40, - 40
820 Data 0,0, xl, xl, 0, 0, - 40, xl
830 DATA 0,0,- 4,twoscore,0,0,- 40,- 40
840 DATA 40, 0, 0, 0, - twoscore, 0, 0.0
850 DATA 0,40,0,0,0,- forty,0,0
860 DATA 0,0,40,0,0,- 40,0
870 Information 0,0,0,40,0,0,0,- 40
920 DATA 1000,1000,1000,1000
1000 LINE (X one, Y1) – (X2, Y2) , 2
1010 GOTO 320
This program has built-in perspective, so that lines more distance from the center are smaller. To remove this perspective modify lines 480, 490, 540, and 550 to:
480 X2=K*(Xc)+158
490 Y2=One thousand*(YC)+100
540 X1=Grand*(90)+158
550 Y1=1000*(YC)+100
This is also true for the previous program the 4D-CUBE. The perspective can exist removed from that program by the same lines in it.
An judge 4D drawing can be made past drawing a 3D drawing of an object twice. And then connecting the point with lines. Fig. 20 shows the 4D coordinate system fatigued this manner.
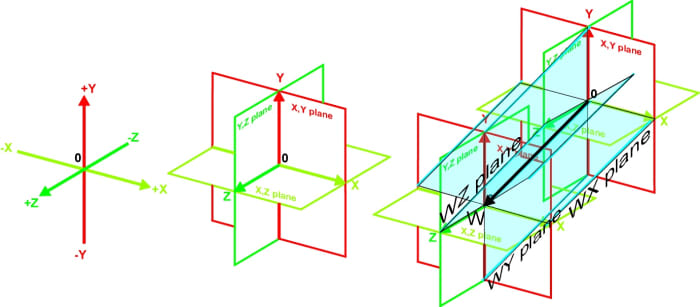
Fig. 20. Iv-dimemsional coordinate system
Fig. 21 shows the 4D tetrahedron, cube and octahedron drawn this fashion.
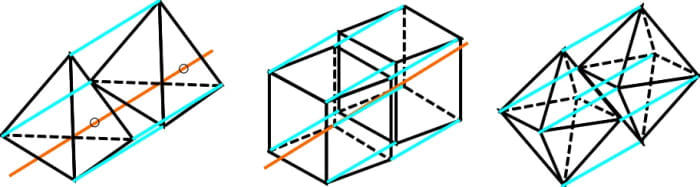
Fig. 21. Iv-dimensional tetrahedron, cube and octahedron
By agreement these principles you can draw all sorts of 4D figures. These tin can be used to study and understand multiple-dimensional systems.
Fourdimensional on Oct 28, 2017:
Rotation in 4-dimensional infinite.
https://youtu.be/vN9T8CHrGo8
The v-cell is an analog of the tetrahedron.
https://youtu.be/z_KnvGGwpAo
Tesseract is a four-dimensional hypercube - an analog of a cube.
https://youtu.be/HsecXtfd_xs
The 16-cell is an analog of the octahedron.
https://youtu.be/1-oj34hmO1Q
The 24-jail cell is 1 of the regular polytope.
https://youtu.exist/w3-TqPXKlVk
The hypersphere is an analog of the sphere.
Mara Alexander from Los Angeles, California on February 27, 2015:
And then kewl, this is admittedly awesome. Cheers for sharing
I voted information technology up
Bennimus - Standing on Oct 29, 2014:
I also forgot to mention. The connect-the-dots play a joke on will piece of work on cubes, but you can't use it on tetrahedrons. You volition get a "tetrahedronal prism". A proper 5-prison cell has v vertices. Aforementioned for octohedrons. Information technology WILL Non WORK unless you want to end upwardly with a prism.
Bennimus on October 29, 2014:
About the 4D graph. At that place's a bit of a blueprint in second representations of college-dimensional graphs.
Generally, the Z axis goes upward. In 2D drawings, Y goes upward. And then where does Y go? It gets squished downward a little bit with the 10 axis.
The same thing happens when we introduce what'south properly known equally a W axis. When the W axis enters the scenario, Information technology points upwards, and it squishes the Z axis alongside the Y and X axes.
All in all it really doesn't matter so long as you have 4 axes, only if you lot're e'er going to do measurements of hypercubes, this is the easiest style to do information technology.
Rahul on August 01, 2013:
Its really so good, but i know this, can you tell me something virtually iv-D sphere. My proper noun is Rahul and my age is fourteen. If you tin tell me something about iv-D sphere than please tell me, this is my ID- planetchachi@gmail.com
Give thanks You lot Sir
Casper on December xxx, 2012:
First-class!, all the same, a 4d tetrahedron has merely five corners!
In your example of a 4d tetrahedron you have fabricated two normal tetrahedrons continued to each other bij xc caste angles into the time.
Zack on February 29, 2012:
I could not exercise any of that! I'thou only in 7th class, and love math, and geometric shapes, but that fabricated no sense. Could you lot make that clearer, delight? my email is lemanski_z@yahoo.com. Thx, Zack.
sve on February 20, 2012:
You lot made it and so simple, it is genius. This is the best explanation of a Fundamental Principle I take seen. Thanks. Continue going.
p johnny joe on November 22, 2011:
sir,it was awesome to see four dimensional figure fabricated by yous,when it is going to come in to activity,tin we make things useful to humanbeings by these figures,100% of the things are made up of 3dimensional,iam a mathematics teacher iam curious to know well-nigh it please write in item to my id johnnyjoe2006@yahoo.com cheers
toxiKrystal on June 06, 2010:
very clear and concise. suprising, considering the amount of usefull informatin hither, as well as the complex nature of fourth-dimentional infinite itself.
i acquired useful noesis and i am sure there is more to learn here. Bookmarked for sure ^-^
... aren't 4dimentional objects stunningly beautiful ^-^ you definitely aided my task of drawing them past mitt.
much thanks
-krys
Mood on May 12, 2010:
Sir you are awesome and passionate, actually benefited from this commodity, thank yous and go along up the awesome work coming !
sinclairnosem1957.blogspot.com
Source: https://feltmagnet.com/drawing/How-to-Draw-Four-Dimensional-Figures
0 Response to "how to draw the number 4 in 3d"
Post a Comment